Mapping Triangles: Understanding Rigid Transformations

Related Articles: Mapping Triangles: Understanding Rigid Transformations

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Mapping Triangles: Understanding Rigid Transformations. Let’s weave interesting information and offer fresh perspectives to the readers.

Mapping Triangles: Understanding Rigid Transformations

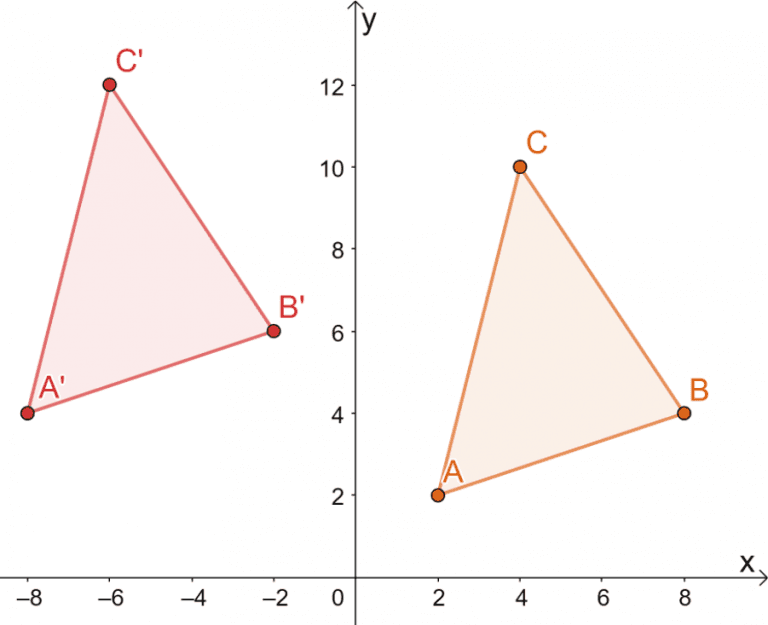
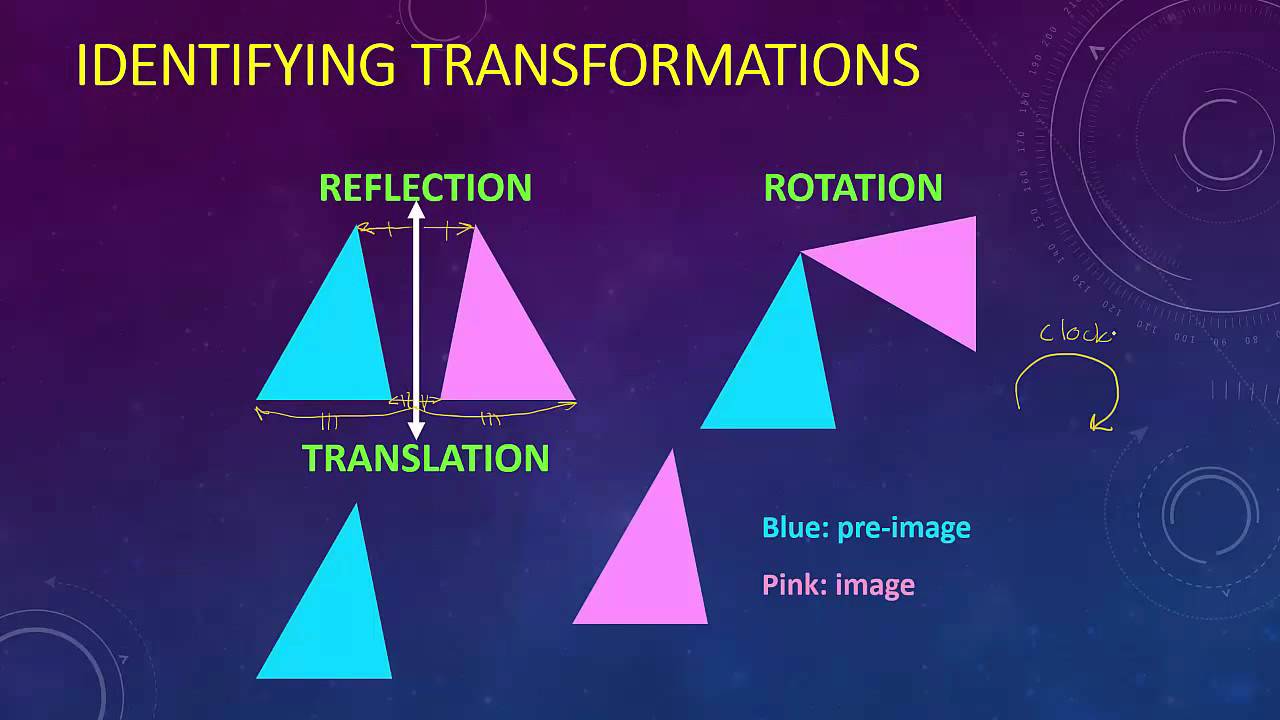
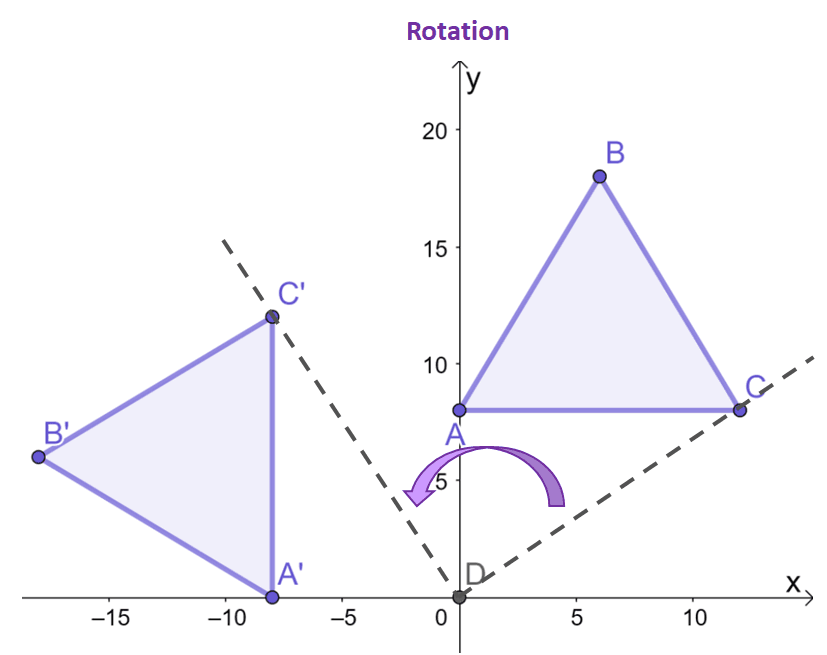
In the realm of geometry, rigid transformations play a crucial role in understanding the relationships between geometric figures. These transformations preserve the size and shape of objects, ensuring that the transformed figure is congruent to the original. One fundamental type of rigid transformation is a translation, which involves moving a figure along a straight line without changing its orientation. Another is a rotation, which involves turning a figure about a fixed point, known as the center of rotation. Finally, a reflection flips a figure across a line, known as the line of reflection.

This article explores how these rigid transformations can be used to map one triangle onto another, specifically focusing on mapping triangle aqr onto triangle akp. By analyzing the corresponding sides and angles of these triangles, we can determine the specific rigid transformation or combination of transformations that will achieve this mapping.

Analyzing the Triangles

To understand the transformation required to map aqr onto akp, we need to examine their corresponding sides and angles:

• Sides:

  • Side aq corresponds to side ak.
  • Side qr corresponds to side kp.
  • Side ar corresponds to side ap.

• Angles:

  • Angle a is common to both triangles.
  • Angle q corresponds to angle k.
  • Angle r corresponds to angle p.

Identifying the Transformation

By carefully comparing the corresponding sides and angles, we can deduce the necessary transformation. Notice that:

• Side lengths: The corresponding sides of aqr and akp are equal in length. This indicates that the transformation does not involve any scaling or dilation.
• Angle measures: The corresponding angles of the two triangles are also equal. This confirms that the transformation preserves the shape of the triangle.

These observations point to a translation as the appropriate transformation to map aqr onto akp. To visualize this, imagine sliding triangle aqr along a straight line until point q coincides with point k. This movement will align the corresponding sides and angles, resulting in a perfect overlap of the two triangles.

The Importance of Rigid Transformations

Understanding rigid transformations holds significant importance in various fields:

• Geometry and Mathematics: Rigid transformations form the foundation of geometric concepts such as congruence, symmetry, and isometries. They are crucial in understanding the properties of shapes and their relationships.

• Computer Graphics and Animation: Rigid transformations are essential in computer graphics for creating realistic animations. By applying translations, rotations, and reflections, objects can be moved, rotated, and flipped, creating dynamic and visually appealing scenes.

• Engineering and Design: Rigid transformations are used in engineering and design to analyze and manipulate structures. They help in understanding the behavior of objects under different conditions and in designing efficient and stable structures.

• Physics and Mechanics: Rigid transformations are fundamental in physics, particularly in mechanics. They are used to describe the motion of rigid bodies, analyzing their displacement, velocity, and acceleration.

Frequently Asked Questions

Q1: Can a single reflection map aqr onto akp?

A: While a reflection can change the orientation of a figure, it cannot be used to map aqr onto akp in this case. A reflection would flip the triangle across a line, resulting in a mirror image. Since the triangles are not mirror images of each other, a single reflection would not achieve the desired mapping.

Q2: Is it possible to map aqr onto akp using a rotation?

A: While a rotation can change the orientation of a figure, it cannot be used to map aqr onto akp in this case. A rotation would turn the triangle about a fixed point. While this could potentially align some of the corresponding sides, it is unlikely to align all sides and angles simultaneously without additional transformations.

Q3: Are there other combinations of rigid transformations that could map aqr onto akp?

A: While a simple translation is the most straightforward solution, other combinations of rigid transformations could potentially achieve the same mapping. For instance, a sequence of two reflections across parallel lines would have the same effect as a translation. However, the translation remains the most efficient and direct way to map aqr onto akp.

Tips for Determining Rigid Transformations

When determining the rigid transformation required to map one figure onto another, consider these tips:

• Analyze corresponding sides and angles: Compare the lengths of corresponding sides and the measures of corresponding angles. This will provide crucial information about the type of transformation needed.
• Consider orientation: Pay attention to the orientation of the figures. Are they mirror images of each other? If so, a reflection may be necessary.
• Visualize the transformation: Imagine how the figures would move to align perfectly. This can help you determine the appropriate type of transformation and its direction.

Conclusion

Mapping triangle aqr onto triangle akp involves a simple translation. This transformation preserves the size and shape of the triangle, ensuring congruence between the original and transformed figures. Understanding rigid transformations is essential in various fields, including geometry, computer graphics, engineering, and physics. By analyzing corresponding sides and angles, we can determine the specific rigid transformation needed to map one figure onto another, unlocking a deeper understanding of geometric relationships and their applications.

Closure

Thus, we hope this article has provided valuable insights into Mapping Triangles: Understanding Rigid Transformations. We thank you for taking the time to read this article. See you in our next article!